



The Dance of Number, in two parts (Part 1, Part 2), two volumes per part with detailed solutions manuals, scope and sequence, quizzes and exams, is now in print.
The Dance of Number is a sequenced and tightly integrated curriculum involving four textbooks totaling 1902 pages (Grades 7-10). The only prerequisite is above average reading comprehension. We start from ground zero, teach the basics of arithmetic from a fresh, vibrant perspective, and then take the reader on a journey that leads to the borderlands of the mountain range called Calculus. There are plenty of side roads along the way where we stop to gaze at the scenic beauty (i.e., a unified look at principles of Algebra, Geometry, Trigonometry). It is a long trip; its completion is worth the effort.
The texts are not named Algebra I or Algebra II, etc., because the four-volume sequence tells a coordinated story engaging the student in the nature of the structure of number, the development of its history, and its interpenetration with science. As the student takes this journey, all the topics of Arithmetic, high school Algebra, most of Geometry, and a complete study of Trigonometry are unfolded.
Because of this harmonized approach, these texts are different than most of what is on the market. The author wants the student to see how the ideas/branches of mathematics interpenetrate (e.g., you are doing algebraic operations and geometrical procedures as you are learning the elements of trigonometry). Our current textbook structure is not that successful at doing this.
After this sequence is completed, the student would be ready either for a complete course in Geometry (if desired) or PreCalculus.
The series is published through Amazon's Createspace. The author page is here.
General Advertising Brochure (27 April 2019) for the Dance of Number curriculum. Print in landscape, double-sided, flip on short edge.
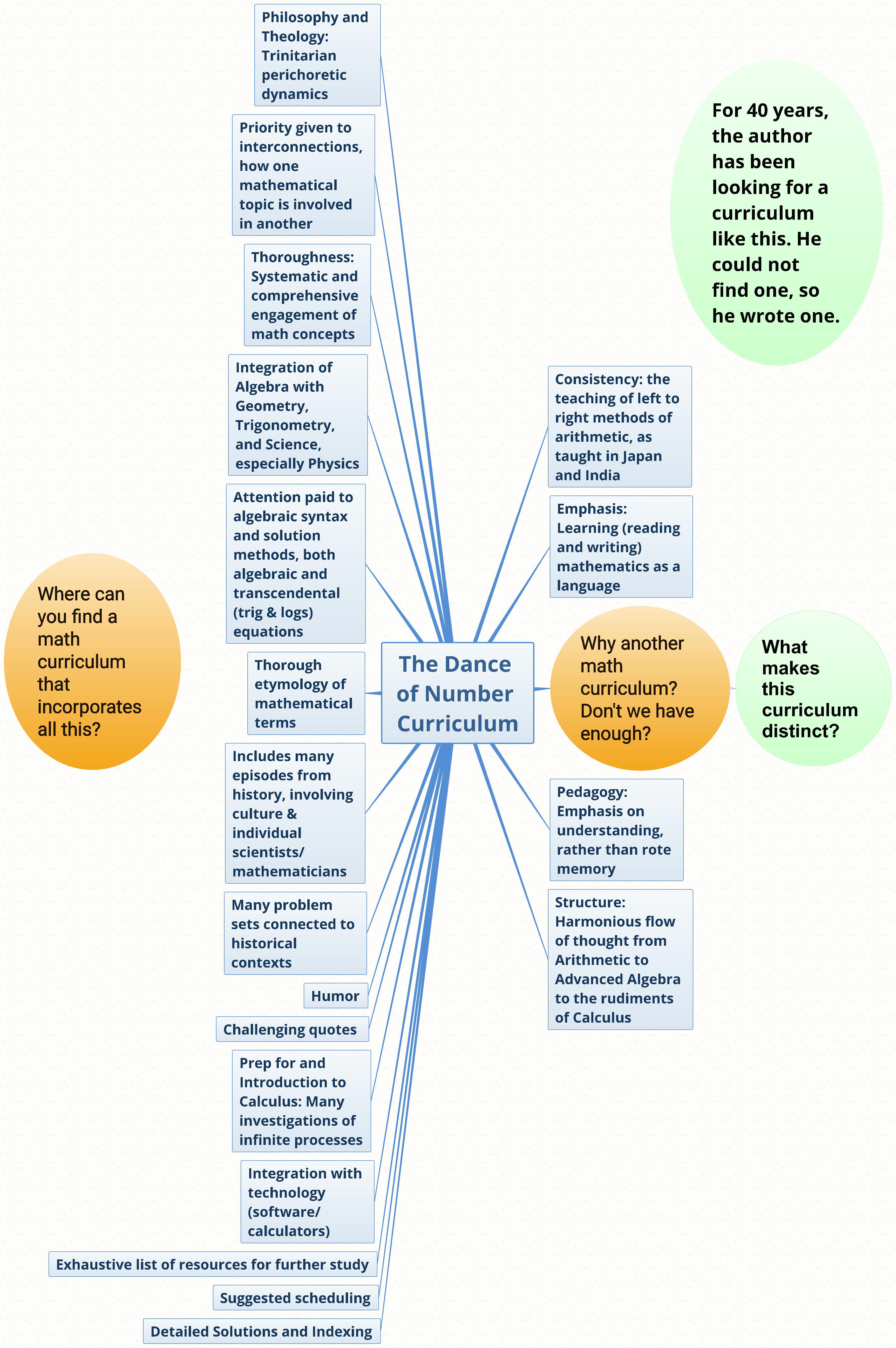
Advertising Brochure: Why another math curriculum? (27 April 2019) for the Dance of Number curriculum. Print in landscape, double-sided, flip on short edge.
FAQ (16 August 2018) for the Dance of Number curriculum. This file will be updated on a regular basis.
ERRATA (16 May 2025) for the Dance of Number curriculum. This file will be updated on a regular basis.
Perichoresis and Mathematics: Mathematics Module - CreatEd Institute (2018)
The Dance of Number is the Way Forward for Teaching Mathematics in the Classical Christian Tradition - Review by Terence Gillespie.
The Dance of Number blog by Kate Deddens.
Interview with James D Nickel, Author of The Dance of Number.
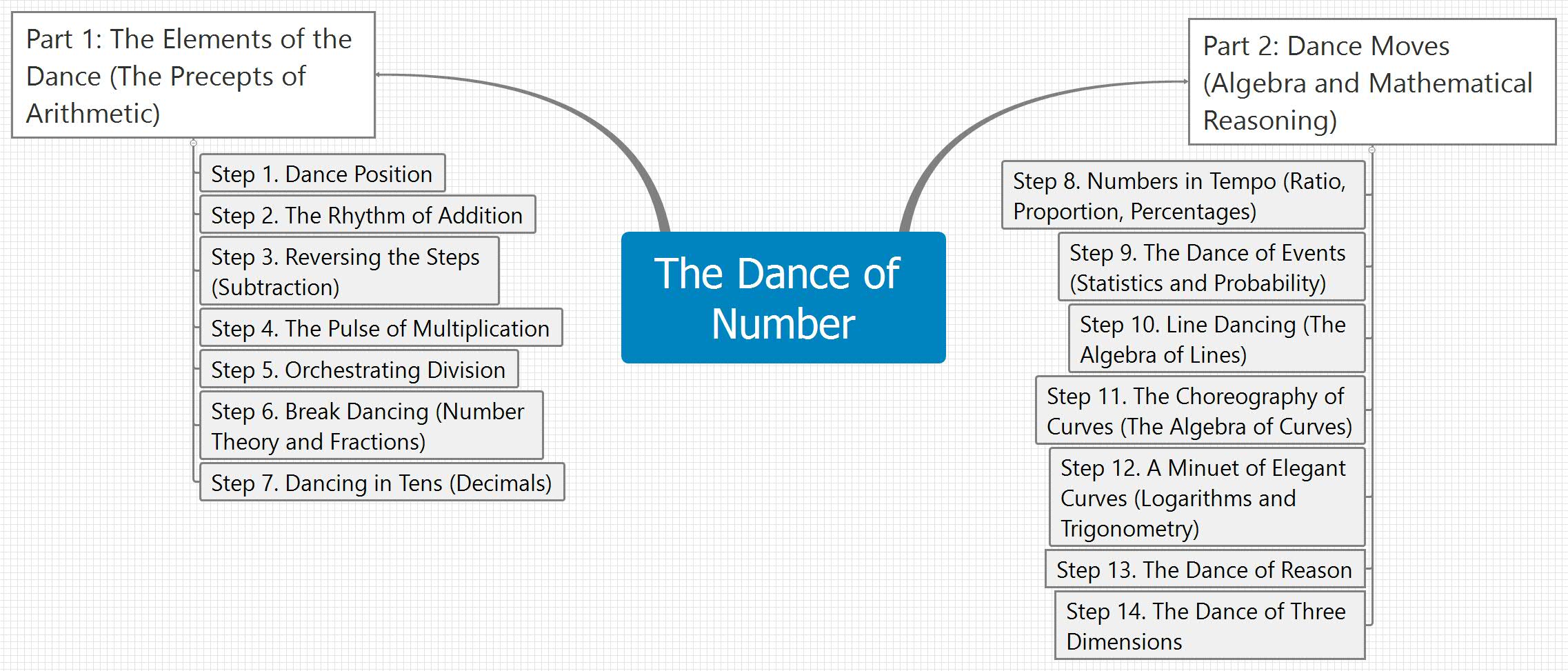
Overview of Math/Science topics taught in The Dance of Number, Four Volumes, Steps 1-14 [Excel format (*.xlsx)].
Why this curriculum resolves Christian Education and the Math Problem.
As a high school teacher of mathematics, I have observed far too many students who can't do algebraic work because they have not mastered Arithmetic. When it comes to dividing by a fraction, many cannot remember what to invert, a symptom of a deeper conceptual issue: "What does it mean to divide a number by a fraction, and what should my answer approximately be?" I have also noted that very few students possess what I call the joy of number sense, i.e., a feel for numbers, the pulse of their patterns - how they work, how they interact, and how they reveal rational order.
Why? Our digital world of calculators and computers that may be at fault. (Note: I am not an opponent of technological progress.) Too often students succumb to pushing buttons instead of doing an addition or multiplication problem in writing. In our world of digital cash registers, when was the last time that you saw a store clerk return change to you by counting backward, one of the lost arts of mental Arithmetic? Maybe our educational system, by experimenting with all kinds of pedagogical fads, has lost its way and lost far too many students to math illiteracy as a result.
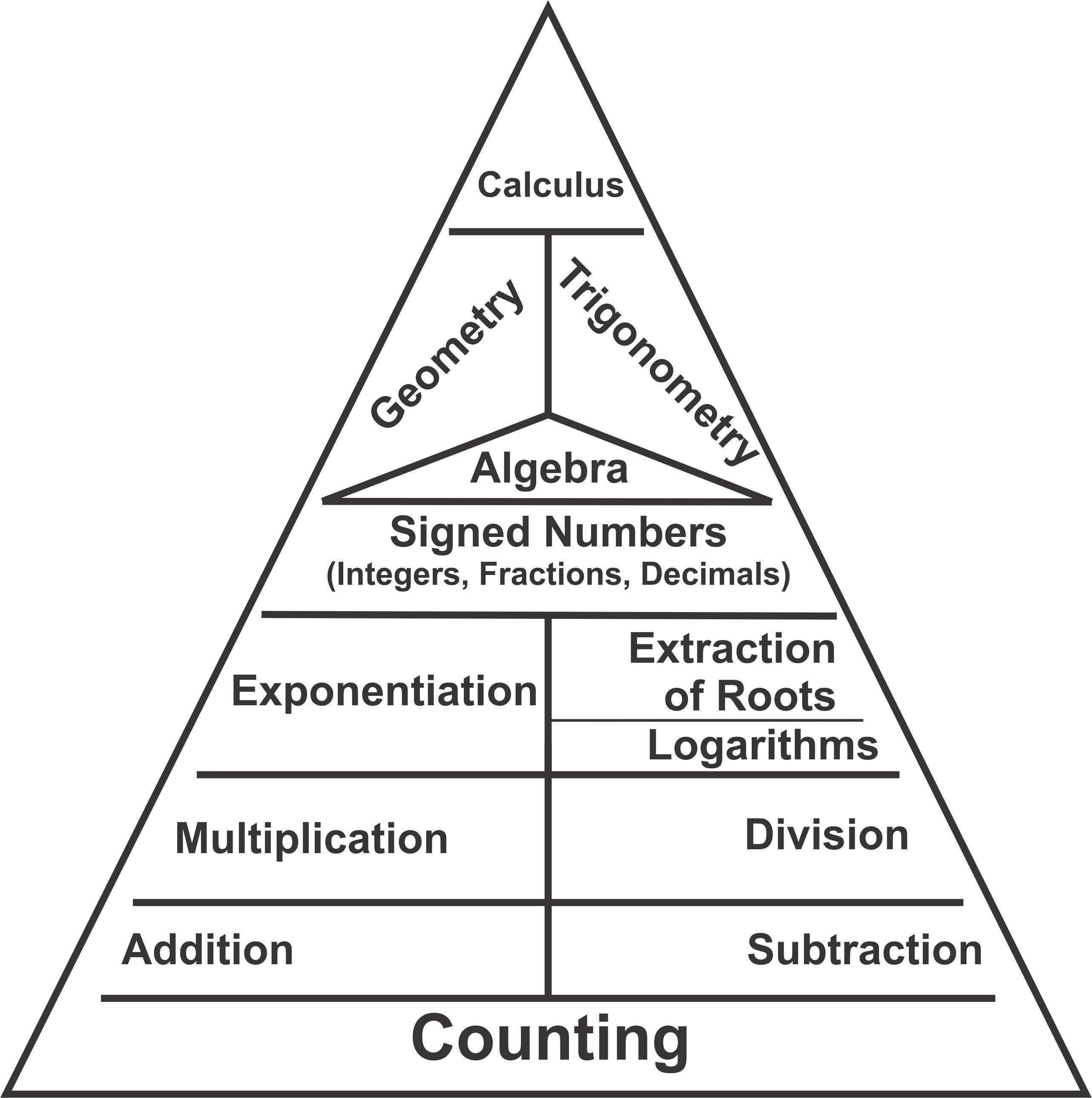
The mastery of arithmetic operations is the foundation for success in Algebra, Geometry, and Trigonometry. We can understand Algebra, as Sir Isaac Newton (1642-1727) observed, as generalized Arithmetic. In Algebra, instead of working with numerals - symbols of the number concept - you are working with symbols of numerals, which are symbols of symbols. These symbols consist of letters that mathematicians combine with numerals. Because mathematics is consistent, you add, subtract, multiply, and divide algebraic symbols in the same way you add, subtract, multiply, and divide numerals in Arithmetic. Algebra, combined with principles of Geometry and Trigonometry, forms the backbone for understanding Calculus, the mathematics of motion at an instant, a method that Newton invented, along with Gottfried Wilhelm Leibniz (1646-1716), when trying to solve scientific problems. The historian Arnold Toynbee (1889-1975) notes the significance of Calculus:
Looking back, I feel sure that I ought not to have been offered the choice [whether to study Greek or Calculus - JN] … calculus ought to have been compulsory for me. One ought, after all, to be initiated into the life of the world in which one is going to live. I was going to live in the Western World … and the calculus, like the full-rigged sailing ship, is … one of the characteristic expressions of the modern Western genius.
[Arnold Toynbee, Experiences (New York: Oxford University Press, 1969), pp. 12-13.]
Calculus is the rigging of the ship of modern science and technology. It is also the foundation of higher branches of mathematical study, subjects you will study in University. From the mountaintop of higher mathematics, you can behold a multitude of rational wonders. To climb to this height is a worthy and achievable goal, but you must master the rudiments of counting and algebraic operations as your first steps in the journey upwards.
The pages that follow examine the dance of number, explorations that will enable you to discern the rhythm of numerical and spatial patterns, both within mathematics and in the physical creation. These investigations begin with the premise that the Triune God of Scripture, the interpenetrating dance of His being, is the ground for those rational patterns. The more you are at home with these patterns, the better you can understand and use the good gifts that God has granted to you in the physical world. If you want to understand the nature and structure of the physical creation, you must master arithmetic and algebraic processes. May the living God bless you with delight and understanding as you endeavor to learn the dance of these patterns.
The reason for the popularity of some math curricula is its ease of use for both students and teachers/parents. These curricula, especially those designed specifically for homeschoolers, are primarily formula- or skill-based. In these curricula, there is little serious interpenetration with history, philosophy, theology, science, or learning to read and write real mathematics, i.e., its syntax.
The only way most math textbooks can achieve popularity is by stooping to the lowest level, i.e., they give the student math formulas or techniques that help the student to get answers to specific types of problems. This approach limits the development of conceptual thinking by trumping the why question with the how question, i.e., methods eclipse justification. Understanding and doing math requires the interplay of two thought components: (1) inductive reasoning, the search for patterns or the derivation of a way to solve a problem and (2) deductive reasoning, the establishment of the absolute truth of certain propositions or the derivation of the correct steps to get the correct answer to a problem. Instead of dictating methods, the student should learn how to discover them via induction and justify them via deduction. Many math curricula sacrifice what is essential in mathematics, problem-solving and critical thinking skills, under the facade of making math easier to learn.
The goal of this math curricula is to develop mathematical utility, the how, in the context of mathematical exploration, how the how is obtained, and mathematical justification, the why.
I came across James Nickel's book Mathematics: Is God Silent? as a Christian Mathematics teacher. His book was like rain in a parched land. I do not think that I overstate the case when I say that reading Mathematics: Is God Silent? was a watershed moment for me as a teacher.
When I was afforded the privilege to work through an advance copy of The Dance of Number, I did so with great anticipation. I was not disappointed. I only wish I had been taught with such a textbook - it would have made the study of Mathematics meaningful and much more interesting. In addition to the excellent pedagogy evident throughout the book, Nickel firmly establishes Mathematics as a field worthy of study by any person interested in thinking God's thoughts after Him.
James Nickel's work will benefit schools, teachers and children across the globe. He has done a service to the body of Christ which will, I believe, prove to be of inestimable value in preparing Christian children to take their rightful place in the world, and in setting aright so much that has gone wrong in education
Hanna Pretorius, HOD Academics, Domino Servite School, South Africa
Work of a lifetime. People are known for their contributions in fields of inquiry, participation in great events, experiments which create discoveries, and ideas which break down walls of unknowing. Few are they whose life work assists in all four.
With James Nickel's latest masterpiece he has given mathematics, publishing, discovery, and think-tank worlds a contribution to which all teachers, students, thinkers, and generations will point. No one has both the breadth of knowledge combined with the educational practice to match Nickel's curriculum. No one ever needs try again.
The Church, the school, the academe, the world should sit up and take notice. Mathematics reflects the language The Father used to create the universe; its principles and truths permeate all of life, every problem, and solution. Jesus, second person of The Trinity, the God-Man, is the source, unification, sustainer, and will be the culmination of all truth. The Spirit now amplifies creation's message to every one of God's creatures: "Look! See! Know! Math is God's witness to earth from Heaven!" All mathematical knowledge throughout creation is intended for Trinitarian glory. James Nickel has held a mirror up to mathematics to announce The Personal Eternal Triune Creator's lordship over all.
Dr. Mark Eckel, President, The Comenius Institute, Indianapolis, Indiana
No field has more frequently been offered as proof of the a-religious nature of vast areas of human knowledge than mathematics, and no scholar has so incisively refuted this notion than James Nickel. In this comprehensive work, Nickel exhibits the inescapably Christian character of mathematics - logical, beautiful, and useful precisely because it is God's creation in the Son. There is no work in history quite like this one - and likely none in the foreseeable future.
P. Andrew Sandlin, Founder & President, Center for Cultural Leadership